image credit: eatuppizza
Part I: Decibels, Impedance, and Operating Level
Audio engineering enthusiasts are often confused by product specifications, which honestly aren’t always helpful, as they can lack comparability between product classes. Here is a primer on three concepts involved in audio signal transmission and how to interpret their specifications into use in the field.
Neophyte audio technicians will quickly learn about two types of amplifiers: “preamps” and “power amps”. Simply speaking, a preamplifier is a device that raises a signal level from a lower level up to line level. That lower level could be from a dynamic or condenser microphone, an instrument with a magnetic or piezoelectric pickup (including contact microphones), or any other sub-line-level device. All of the listed devices are transducers, meaning they convert acoustic energy into an electronic signal.
A power amplifier is a device that converts a line-level input signal into a powered output capable of driving speakers (or headphones) to the required volume for sound reproduction. Preamplifiers and power amplifiers can be combined into a single device, if desired. An example is a powered mixer, which may have microphone, instrument, and line level inputs, and may route separate mixes to line level, headphone, and speaker-level outputs.
Having defined these basic types of amplifiers, let’s chart the operating levels of each. But first, a quick primer on decibel measurements!
Decibels and audio signal measurement
A decibel is one-tenth of a Bel (named after Alexander Graham Bell), which is a unit of sound intensity. It is also used as a reference for signal strength.
Decibels are a logarithmic representation of comparative signals. This is useful because audio signals have a very wide range of signal strength, from less than 1μV (microvolt) to 100V! In decibels, that is -120dBV to +40dBV. Using a log scale converts mathematical operations from multiplication and division to addition and subtraction. Math is hard! So we use decibels to make audio measurements and comparisons easier.
To convert a signal voltage to decibels, use this equation:
dB = 20 * log (V1 / V2)
(for power comparison, in watts, the equation is 10 * log (W1 /W2))
Note that a decibel measurement is always a comparison; either to an absolute or relative reference. For example, we can say that a signal is 10dB stronger than another signal. If we want that reference to be absolute, we can indicate that with a standard designation, such as dBV, dBm, dBu, dBSPL, or dBFS:
dBV = in comparison with a reference signal of 1VRMS (root-mean-square, such that a sine wave of 2.83V peak-to-peak, or Vpp, will be 1VRMS). dBV is the most common reference used in microphone specifications, and I argue is the most useful reference in modern audio engineering, as many analog to digital converter ICs have a 0dBFS signal set very close to 0dBV (see below). dBV is also the reference for the “consumer” operating level of -10dBV.
dBm = in comparison with a signal that will generate 1mW of power into a standard load. For an audio signal, that load is assumed to 600Ω (for radio frequency signals, it will be the characteristic impedance of the circuit, often 50Ω, but other impedances are also common). This is not relevant any longer in audio engineering, since most modern audio amplifiers have an input impedance much greater than 600Ω, and an output impedance much lower. However, it is sometimes still used by those accustomed to vintage equipment, as an equivalent term to dBu, below.
dBu = u is for “unit”, as it was a reference to old-school VU meters, but you may think of it as “unloaded” for a good mnemonic. It refers to the signal voltage that would yield 1mW into 600Ω, except the signal is considered to have no load. To illustrate these last two concepts, let’s derive 0dBm for an audio signal, using the power equation:
P (power, in watts) = I (current, in amps) * V (voltage)
We are given 1mW and 600Ω, so we have to solve for current and voltage using Ohm’s Law:
I = V / R (resistance, in ohms)
Substituting:
P = V * I
P = V * (V/R)
0.001W = V * V / 600Ω
V ^ 2 = 0.6
V = 0.775
Thus, 0dBu is 0.775V, which is the voltage into 600Ω that will produce power of 1mW.
dBu is still commonly used as a reference for microphone preamplifiers, which creates an inherent difficulty in comparing specifications—the reference voltages are different:
dB = 20 * log (1V / 0.775V) = 2.2dB
Such that 0dBV is +2.2dB in comparison with 0dBu; that is, 0dBV = +2.2dBu, and 0dBu = -2.2dBV. We’ll explore the consequence of that difference in the section below on operating levels.
dBSPL is an acoustic measure, “Sound Pressure Level”. It is an absolute measure in reference to Pascals (the standard unit of pressure), as:
1Pa = 94dBSPL
dBSPL is an important reference for the efficiency of microphones converting acoustic energy into electrical energy. A given microphone’s efficiency in that conversion is stated as the microphone’s “sensitivity”, relative to 1Pa.
The range of human hearing is generally stated as 0dBSPL to 140dBSPL, those extremes representing the extremes of the quietest sounds possible to hear and acute physical pain. These of course vary according to frequency as well as the individual’s hearing acuity. In a sound reinforcement and recording applications, it may be necessary for a microphone to tolerate even louder sounds, such as when using close placements on drums.
An important concept is that an SPL measurement is always a point measurement, because sound from a point source in free space will decrease in pressure with the square of distance (6dB per doubling of distance). It’s not quite the same dropoff if you’re not in free space, because of reflected sound, and not every sound source is a point. That said, if you’re at a concert that is 110dBSPL at your seat, the sound pressure at the PA speaker will be much, much higher! Keep that principle in mind when selecting microphones for close-mic applications!
Finally, dBFS is a reference for a digital signal, to the signal that will generate a “full scale” range at the audio to digital converter (ADC). Since most ADCs operate on a power supply of between 3.3V and 5V, nominally dBFS should be in the range of 0dBV to +5dBV. However, since ADCs are expected to operate with a line-level input which may be +20dB stronger, professional digital audio devices will have the ability to attenuate the input signal before their ADC circuitry. Thus, each ADC will have its own specification for dBV (or dBu) = 0dBFS.
Digital to analog converters (DACs) will operate the same, in reverse: The output level of 0dBV to +5dBV at the DAC will be increased to the required operating level by the following analog output circuit.
Impedance
Impedance is an important factor in signal transmission that is often not well understood. Sometimes described as “AC resistance”, impedance is a complex measurement of frequency-dependent resistance to electrical current. The impedance of a device can be different at various frequencies; although for many audio devices, impedance will be constant across much or all of the audio frequency band.
An audio device may have a figure given for input (load) impedance, output (source) impedance, or both. Source impedance can be considered as that device’s ability to supply current, and load impedance is that device’s demand for current.
In modern audio interconnection, systems are designed to minimize signal losses within normal ranges of impedance. This is referred to as impedance bridging, in contrast to impedance matching (which is important in radio frequency signal transmission) that maximizes power transfer.
In bridging impedance, a device’s source impedance is intended to be significantly lower than the load impedance of the following device, so that an excessive amount of signal is not lost in transmission. Nominally, this is about a difference of ten: for example, the standard source impedance for a professional microphone is 150Ω, and the standard load impedance for a microphone amplifier is 1.5kΩ. This yields a mere loss of -0.8dB in transmission—in case you want to see that math:
20 * log ( 1500 Ω / 1650 Ω) = -0.8dB
In practice, microphone amplifier models may vary from 600Ω to 3KΩ input impedance, or even higher. Some amplifiers provide a variable or selectable low input impedance, even down to 150Ω, for those applications were impedance matching is desired.
Instrument pickups and amplifiers follow the same logic, just with higher figures. A typical magnetic pickup is around 5kΩ to 15kΩ source impedance, and an instrument amplifier is often 1MΩ or more. That is strictly more than needed for the pickup, but once a volume pot on a passive instrument is engaged, the source impedance of the instrument can be over 100kΩ! Also, since a magnetic pickup uses a coil, it is an inductive source, which means a complex impedance—in this case, increasing as frequency increases. So the high input impedance of the amplifier minimizes the change in signal loss with frequency.
There are some instances in audio signal transmission where impedance matching is desirable, mostly where coils are involved (dynamic microphones and output transformers). This is beyond the scope of this article (I have to leave something out)!
Operating Level and Amplification
Microphones have a wide range for their sensitivity specification; again, this is the measure of efficiency in converting acoustic energy to an electrical signal, and depends on both the operating principle of the microphone capsule (dynamic, condenser, etc.), as well as the microphone’s internal circuitry (active circuits, transformers). The specification for sensitivity is given at 1Pa, or 94dBSPL, which is the standard acoustic operating level. Typical operating levels for microphones:
Dynamic (moving coil or ribbon): -60dBV/Pa to -45dBV/Pa
Condenser: -45dBV/Pa to -25dBV/Pa
Thus, condenser microphones are usually about 20dB “hotter” than dynamic microphones.
Instrument level also depends on the type of transducer; single-coil pickups will be the lowest, at perhaps -30dBV; dual-coil humbuckers will be nominally 6dB higher. Active pickups will be higher still, and piezoelectric (“contact”) pickups can be similar, nominally at -20dBV.
A preamplifier can be capable of supporting any or all types of transducers, although each has somewhat different needs for care and feeding.
The job of the microphone or instrument amplifier is to provide a suitably high load impedance and enough voltage gain—nominally +20dB to +60dB, but will vary according to actual source SPL—so that the output signal is “line level”. It must also provide enough current gain such that it will have a suitably low output impedance.
Line level is defined as either “consumer”, at -10dBV, or “professional”, at +4dBu. That figure is the nominal signal level desired as the input to a power amplifier or a following line level device. As we have seen that the difference between dBV and dBu is 2.2dB, professional level converts to +1.8dBV.
Vintage audio equipment was often designed to match impedance (both source and load would be 600Ω), so dBm was the commonly used measure. As equipment changed to bridge impedance, dBu nominally replaced dBm, to indicate that impedance matching was not expected. So while the 0.775V reference is no longer relevant, it’s still the common measure for professional audio line-level equipment. This creates a difference of 2.2dB from microphones, which are almost universally specified in dBV—keep that in mind when comparing operating levels! (I believe that dBV should be used as the common reference for all small-signal audio devices, with 0dBV as the nominal professional operating level)
Headroom is the difference between that nominal level and the maximum level of the device. Much professional audio equipment operates on a 30Vpp supply, which yields a maximum input of about +20dBV (or +22dBu), for 18dB of headroom. Consumer gear might operate only on a 5Vpp supply, for a maximum level of +5dBV, and thus only 15dB of headroom, although higher headroom consumer devices are common.
In modern equipment, nominal line-level load impedance is 10kΩ, and nominal line-level source impedance, similar to microphones, is 150Ω (but often lower in practice). Thus, very little signal is lost in line-level transmission, and also due to the high signal level, several line-level devices may thus be chained or run in parallel with little signal degradation.
In summary, the job of the preamplifier is to limit signal losses by bridging impedance, add the required amount of voltage gain to raise the signal to line level, and provide enough current gain for a suitably low source impedance at its output to drive the load impedance of the following equipment, whether a power amplifier, ADC, or other line-level input device.
Power amplifiers are normally specified in their maximum output (either continuous, which is preferred, but sometimes listed as peak), into specified loads, in watts. For example, 500W per channel into 8Ω, 750W per channel into 4Ω, or 1500W “bridged” into 8Ω (bridging involves using two channels of a amplifier to drive a single speaker, with a differential signal). If you work backwards, you can derive the voltage levels in those examples, and you’d see how much voltage gain would be necessary from their line-level inputs (sometimes none, sometimes a lot!). Of course, a power amplifier will always need a lot of current gain, because its output impedance has to be a fraction of an ohm to bridge impedance to the speaker.
It would probably be helpful if power amplifiers were specified in dB! dBW maybe? But somehow the narrative got lost there . . .
Stay tuned for:

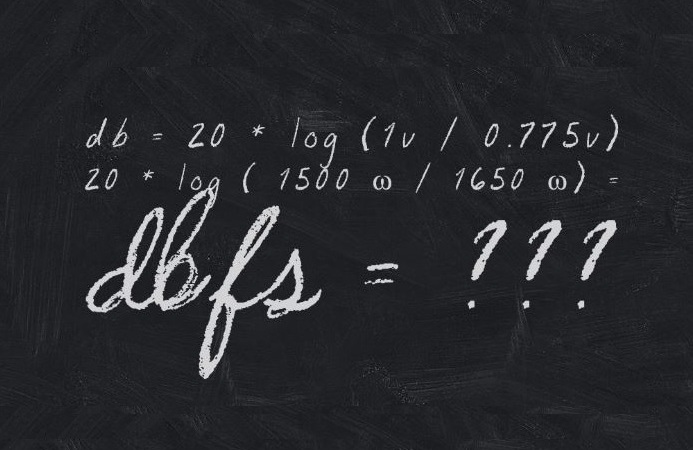
I need the technical expertise of a professional that can solve a problem. I have a voice fire alarm system. When the digital voice message is played on the speakers the db loudness is fine. When i use the microphone, the sound is barely audible. What is the problem?
This is probably a signal level mismatch; your microphone outputs microphone level (could be as low as -60dBV/Pa), but the alarm system expects a line-level signal (-10dBV or higher). You need an appropriate microphone preamplifier between the microphone and the alarm system input.